Mélytanulás könyv - Hu

2. A neurális hálózatok matematikai építőkövei

Ez a fejezet ezekkel foglalkozik:

A mélytanulás megértéséhez sok egyszerű matematikai fogalom ismerete szükséges: tenzorok, tenzorműveletek, differenciálás, gradiens ereszkedés stb. Ebben a fejezetben az lesz a célunk, hogy kiépítsük az intuíciót ezekkel a fogalmakkal kapcsolatban anélkül, hogy túlzottan technikai jellegűvé válnánk. Különösen kerüljük a matematikai jelölést, amely szükségtelen akadályokat állíthat fel azok számára, akik nem rendelkeznek matematikai háttérrel, és nem szükséges jól elmagyarázni a dolgokat. A matematikai műveletek legpontosabb, legegyértelműbb leírása a végrehajtható kód. Ahhoz, hogy elegendő kontextust biztosítsunk a tenzorok és a gradiens ereszkedés bemutatásához, a fejezetet egy neurális hálózat gyakorlati példájával kezdjük. Ezután minden bevezetett új koncepciót pontról pontra átnézünk. Ne feledje, hogy ezek a fogalmak nélkülözhetetlenek lesznek a következő fejezetekben található gyakorlati példák megértéséhez!

{27.o:} Miután elolvasta ezt a fejezetet, intuitív módon megérti a mélytanulás mögött meghúzódó matematikai elméletet, és készen áll arra, hogy a 3. fejezetben belemerüljön a Keras és a TensorFlow témakörbe.

2.1. Első pillantás egy neurális hálózatra

Nézzünk egy konkrét példát egy neurális hálózatra, amely a Python Keras könyvtárat használja a kézzel írt számjegyek osztályozásának megtanulására. Hacsak nincs már tapasztalata a Keras vagy hasonló könyvtárakkal kapcsolatban, nem fog azonnal mindent megérteni erről az első példáról. Ez rendben van így. A következő fejezetben a példa minden elemét áttekintjük, és részletesen elmagyarázzuk. Tehát ne aggódjon, ha egyes lépések önkényesnek vagy varázslatosnak tűnnek! Valahol el kell kezdenünk.

A probléma, amit itt próbálunk megoldani, az, hogy a kézzel írt számjegyek (28 × 28 pixeles) szürkeárnyalatos képeit a 10 kategóriájukba (0-tól 9-ig) besoroljuk. A gépi tanulási közösség klasszikusának számító MNIST adatkészletet fogjuk használni, amely majdnem olyan régóta létezik, mint maga a terület, és intenzíven tanulmányozták. Ez egy 60 000 képzési képből és 10 000 tesztképből álló készlet, amelyet a National Institute of Standards and Technology (a NIST az MNIST-ben) állított össze az 1980-as években. Az MNIST „megoldását” a mélytanulás „Hello Worldjének” tekintheti – ezzel ellenőrizni tudja, hogy az algoritmusok a várt módon működnek-e. Ahogy gépi tanulással foglalkozó gyakornok lesz, az MNIST újra és újra megjelenik a tudományos közleményekben, blogbejegyzésekben stb. Néhány MNIST mintát láthat a 2.1. ábrán.

2.1. ábra: MNIST minta számjegyek

MEGJEGYZÉS

A gépi tanulásban egy osztályozási probléma kategóriáját osztálynak nevezzük. Az adatpontokat mintáknak nevezzük. Az adott mintához tartozó osztályt címkének nevezzük.

Ne akarja most megpróbálni reprodukálni ezt a példát a gépén. Ha szeretné, először be kell állítania egy mélytanulási munkaterületet, amelyről a 3. fejezetben olvashat. Az MNIST-adatkészlet a Kerasba előre telepítve, négy NumPy-tömbből álló készlet formájában érkezik.

2.1. lista: Az MNIST adatkészlet betöltése Kerasba

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images és train_labels alkotják a betanítási halmazt, azokat az adatokat, amelyekből a modell tanulni fog. A modell ezután tesztelésre kerül a test_images és a test_labels tesztkészleten. {28.o:} A képek NumPy tömbökként vannak kódolva, a címkék pedig számjegyek 0-tól 9-ig terjedő tömbjei. A képek és a címkék egy az egyben megfelelnek.

Nézzük a képzési adatokat:

>>> train_images.shape
(60000, 28, 28)
>>> len(train_labels)
60000
>>> train_labels
array([5, 0, 4, ..., 5, 6, 8], dtype=uint8)

És itt vannak a tesztadatok:

>>> test_images.shape
(10000, 28, 28)
>>> len(test_labels)
10000
>>> test_labels
array([7, 2, 1, ..., 4, 5, 6], dtype=uint8)

A munkafolyamat a következő lesz: Először is betápláljuk a neurális hálózatba a train_images és train_labels betanítási adatokat. A hálózat ezután megtanulja társítani a képeket és a címkéket. Végül megkérjük a hálózatot, hogy készítsen előrejelzéseket a test_images számára, és ellenőrizzük, hogy ezek az előrejelzések egyeznek-e a test_labels címkéivel.

Építsük fel a hálózatot – ne feledje, hogy még nem várható el, hogy mindent megértsen ebből a példából.

2.2. lista: A hálózati architektúra

from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
    layers.Dense(512, activation="relu"),
    layers.Dense(10, activation="softmax")
])

A neurális hálózatok alapvető építőköve a réteg. A réteget az adatok szűrőjének tekintheti: bizonyos adatok bekerülnek, és hasznosabb formában kerülnek ki. Pontosabban, a rétegek reprezentációkat vonnak ki a beléjük betáplált adatokból – remélhetőleg olyan reprezentációkat, amelyek értelmesebbek az adott probléma szempontjából. A mélytanulás nagy része egyszerű rétegek összeláncolásából áll, amelyek a progresszív adatdesztilláció egy formáját valósítják meg. A mélytanulási modell olyan, mint az adatfeldolgozás szitája, amely egyre finomabb adatszűrőkből – a rétegekből – áll.

Itt a modellünk két sűrű réteg sorozatából áll, amelyek sűrűn összefüggő (más néven teljesen összefüggő) idegi rétegek. A második (és utolsó) réteg egy 10-utas softmax osztályozási réteg, ami azt jelenti, hogy 10 valószínűségi pontszámból álló tömböt fog visszaadni (összeadva 1-et). Minden pontszám annak a valószínűsége lesz, hogy az aktuális számjegyű kép a 10 számjegyű osztályunk valamelyikébe tartozik. {29.o:}

Ahhoz, hogy a modell képzésre kész legyen, további három dolgot kell kiválasztanunk az összeállítási lépés részeként:

2.3. lista: Az összeállítás lépése

model.compile(optimizer="rmsprop",
              loss="sparse_categorical_crossentropy",
              metrics=["accuracy"])

A képzés előtt az adatokat a modell által elvárt alakra alakítjuk át, és úgy méretezzük, hogy minden érték a [0, 1] intervallumban legyen. Korábban a képzési képeinket egy uint8 típusú alaktömbben (60000, 28, 28) tároltuk [0, 255] intervallumban. Átalakítjuk egy float32 alakú tömbbe (60000, 28 * 28), 0 és 1 közötti értékekkel.

2.4. lista: A képadatok előkészítése

train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255

Most már készen állunk a modell betanítására, ami a Kerasban a modell fit() metódusának meghívásával történik – most illesztjük a modellt a betanítási adataihoz.

2.5. lista: A modell „illesztése”

>>> model.fit(train_images, train_labels, epochs=5, batch_size=128)
Epoch 1/5
60000/60000 [===========================] - 5s - loss: 0.2524 - acc: 0.9273
Epoch 2/5
51328/60000 [=====================>.....] - ETA: 1s - loss: 0.1035 - acc: 0.9692

A betanítás során két mennyiség jelenik meg: a modell vesztesége a betanítási adatok felett, és a modell pontossága a betanítási adatok felett. A képzési adatokon gyorsan elérjük a 0,989-es (98,9%-os) pontosságot.

Most, hogy van egy betanított modellünk, felhasználhatjuk új számjegyek osztályvalószínűségének előrejelzésére – olyan képekre, amelyek nem képezték a betanítási adatok részét, például a tesztkészletből. {30.o:}

2.6. lista: A modell használata előrejelzések készítéséhez

>>> test_digits = test_images[0:10]
>>> predictions = model.predict(test_digits)
>>> predictions[0]
array([1.0726176e-10, 1.6918376e-10, 6.1314843e-08, 8.4106023e-06,
       2.9967067e-11, 3.0331331e-09, 8.3651971e-14, 9.9999106e-01,
       2.6657624e-08, 3.8127661e-07], dtype=float32)

Ebben a tömbben az i indexek minden száma megfelel annak a valószínűségének, hogy a test_digits[0] számjegykép az i. osztályba tartozik.

Ennek az első tesztszámjegynek a legmagasabb a valószínűségi pontszáma (0,99999106, majdnem 1) a 7-es indexnél, tehát modellünk szerint 7-nek kell lennie:

>>> predictions[0].argmax()
7
>>> predictions[0][7]
0.99999106

Ellenőrizni tudjuk, hogy a tesztcímke megegyezik-e:

>>> test_labels[0]
7

Átlagosan mennyire jó a modellünk az ilyen soha nem látott számjegyek osztályozásában? Ellenőrizzük a teljes tesztkészlet átlagos pontosságának kiszámításával.

2.7. lista: A modell kiértékelése új adatokon

>>> test_loss, test_acc = model.evaluate(test_images, test_labels)
>>> print(f"test_acc: {test_acc}")
test_acc: 0.9785

A tesztkészlet pontossága 97,8% - ez egy kicsit kisebb, mint a képzési készlet pontossága (98,9%). A képzési pontosság és a tesztpontosság közötti különbség a túlillesztés példája: az a tény, hogy a gépi tanulási modellek általában rosszabbul teljesítenek az új adatokon, mint a betanítási adatokon. A túlillesztés a 3. fejezet központi témája.

Ezzel végére is értünk az első példánknak – most láttad, hogyan tudsz felépíteni és betanítani egy neurális hálózatot, hogy a kézzel írt számjegyeket osztályozza, és mindezt kevesebb, mint 15 Python-kódsorban. Ebben és a következő fejezetben részletesen kitérünk minden alkotórészre, amelyet most előre megnéztünk, és tisztázzuk, mi történik a színfalak mögött. Megismerheti a tenzorokat, a modellbe kerülő adattároló objektumokat; tenzorműveleteket, mely rétegekből készülnek; és a gradiens ereszkedést, amely lehetővé teszi, hogy modellje tanuljon a képzési példákból. {31.o:}

2.2. Adatábrázolások neurális hálózatokhoz

Az előző példában többdimenziós NumPy tömbökben, más néven tenzorokban tárolt adatokból indultunk ki. Általában minden jelenlegi gépi tanulási rendszer tenzorokat használ alapvető adatszerkezetként. A tenzorok alapvetőek a területen – annyira alapvetőek, hogy a TensorFlow-t róluk nevezték el. Tehát mi a tenzor? A tenzor lényegében egy adattároló – mégpedig általában numerikus adatok. Tehát ez egy számtároló. Lehet, hogy már ismeri a mátrixokat, amelyek 2. rangú tenzorok: a tenzorok a mátrixok tetszőleges számú dimenzióra történő általánosítása (megjegyzendő, hogy a tenzorokkal összefüggésben egy dimenziót gyakran tengelynek neveznek).

2.2.1 Skalárok (nulladrendű tenzorok)

A csak egy számot tartalmazó tenzort skalárnak (vagy skalártenzornak, vagy nulladrendű tenzornak vagy 0D tenzornak) nevezzük. A NumPy-ban a float32 vagy float64 szám skalártenzor (vagy skalártömb). A NumPy tenzor tengelyeinek számát az ndim attribútummal tudjuk megjeleníteni; egy skaláris tenzornak 0 tengelye van (ndim == 0). A tenzor tengelyeinek számát rendjének is nevezik. Íme egy NumPy skalár:

>>> import numpy as np
>>> x = np.array(12)
>>> x
array(12)
>>> x.ndim
0

2.2.2 Vektorok (elsőrendű tenzorok)

A számokból álló tömböt vektornak, elsőrendű tenzornak vagy 1D tenzornak nevezzük. Egy elsőrendű tenzornak pontosan egy tengelye van. A következő egy NumPy vektor:

>>> x = np.array([12, 3, 6, 14, 7])
>>> x
array([12, 3, 6, 14, 7])
>>> x.ndim
1

Ennek a vektornak öt bejegyzése van, ezért 5-dimenziós vektornak nevezik. Ne keverje össze az 5D vektort az 5D tenzorral! Egy 5D vektornak csak egy tengelye van, és a tengelye mentén öt dimenziója, míg az 5D tenzornak öt tengelye van (és tetszőleges számú dimenziója lehet minden tengely mentén). A dimenzionalitás jelölheti vagy egy adott tengely mentén lévő bejegyzések számát (mint az 5D vektorunk esetében), vagy egy tenzor tengelyeinek számát (például egy 5D tenzor), ami időnként zavaró lehet. Ez utóbbi esetben technikailag helyesebb ötödrendű tenzorról beszélni (a tenzor rangja a tengelyek száma), de ettől függetlenül gyakori az 5D tenzor kétértelmű jelölés. {32.o:}

2.2.3 Mátrixok (másodrendű tenzorok)

A vektorok tömbje egy mátrix, vagy másodrendű tenzor vagy 2D tenzor. A mátrixnak két tengelye van (ezeket gyakran sornak és oszlopnak nevezik). A mátrixot vizuálisan értelmezheti téglalap alakú számrácsként. Ez egy NumPy mátrix:

>>> x = np.array([[5, 78, 2, 34, 0],
                  [6, 79, 3, 35, 1],
                  [7, 80, 4, 36, 2]])
>>> x.ndim
2

Az első tengely bejegyzéseit soroknak, a második tengely bejegyzéseit oszlopoknak nevezzük. Az előző példában [5, 78, 2, 34, 0] az x első sora, és az [5, 6, 7] az első oszlopa.

2.2.4. Harmad- és magasabb rendű tenzorok

Ha az ilyen mátrixokat egy új tömbbe csomagoljuk, akkor egy harmadrendű tenzort (vagy 3D tenzort) kapunk, amelyet vizuálisan számkockaként értelmezhetünk. A következő egy NumPy harmadrendű tenzor:

>>> x = np.array([[[5, 78, 2, 34, 0],
                   [6, 79, 3, 35, 1],
                   [7, 80, 4, 36, 2]],
                  [[5, 78, 2, 34, 0],
                   [6, 79, 3, 35, 1],
                   [7, 80, 4, 36, 2]],
                  [[5, 78, 2, 34, 0],
                   [6, 79, 3, 35, 1],
                   [7, 80, 4, 36, 2]]])
>>> x.ndim
3

Ha a harmadrendű tenzorokat egy tömbbe csomagolja, létrehozhat egy negyedrendű tenzort, és így tovább. A mélytanulás során általában a 0-tól 4-ig terjedő tenzorokat kell manipulálni, de ez akár 5-ig is felmehet, ha videoadatokat dolgoz fel.

2.2.5 Kulcs attribútumok

A tenzort három fő attribútum határozza meg:

Hogy ezt konkrétabbá tegyük, tekintsünk vissza az MNIST példában feldolgozott adatokra. Először betöltjük az MNIST adatkészletet:

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

Ezután megjelenítjük a train_images tenzor tengelyeinek számát, az ndim attribútumot:

>>> train_images.ndim
3

Íme az alakja:

>>> train_images.shape
(60000, 28, 28)

És az adattípusa, a dtype attribútum:

>>> train_images.dtype
uint8

Tehát itt van egy 8 bites egész számokból álló harmadrendű tenzor. Pontosabban, ez egy 60 000 darab 28 × 28 egész számból álló mátrixból felépített tömb. Mindegyik ilyen mátrix egy szürkeárnyalatos kép, 0 és 255 közötti értékű pixelekkel.

Jelenítsük meg a negyedik számjegyet ebben a harmadrendű tenzorban a Matplotlib könyvtár segítségével (ami egy jól ismert Python adatvizualizációs könyvtár, amely előre telepítve van a Colabban); lásd a 2.2 ábrát.

2.2. ábra: Adatkészletünk negyedik mintája

2.8. lista: A negyedik számjegy megjelenítése

import matplotlib.pyplot as plt
digit = train_images[4]
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()

Természetesen a megfelelő címke a 9-es egész szám:

>>> train_labels[4]
9

2.2.6 Tenzorok manipulálása a NumPy-ban

Az előző példában kiválasztottunk egy adott számjegyet az első tengely mellett a train_images[i] szintaxis használatával. A tenzorban meghatározott elemek kiválasztását tenzorszeletelésnek nevezzük. Nézzük meg a tenzorszeletelési műveleteket, amelyeket a NumPy tömbökön végezhet. A következő példa a #10-től #100-ig terjedő számjegyeket választja ki (a #100 nem szerepel), és egy (90, 28, 28) alakú tömbbe helyezi őket :

>>> my_slice = train_images[10:100]
>>> my_slice.shape
(90, 28, 28)

Ez egyenértékű ezzel a részletesebb jelöléssel, amely minden tenzortengely mentén meghatároz egy kezdő- és egy végindexet a szelethez. Vegye figyelembe, hogy a : egyenértékű a teljes tengely kiválasztásával:

>>> my_slice = train_images[10:100, :, :]  <--- Egyenértékű az előző példával
>>> my_slice.shape
(90, 28, 28)
>>> my_slice = train_images[10:100, 0:28, 0:28] <---Szintén egyenértékű az  
                                                    előző példával
>>> my_slice.shape
(90, 28, 28)

Általában az egyes tenzortengelyek mentén tetszőleges két index közül választhat szeleteket. Ha például az összes kép jobb alsó sarkában 14 × 14 képpontot szeretne kiválasztani, tegye a következőket:

my_slice = train_images[:, 14:, 14:]

Lehetőség van negatív indexek használatára is. Hasonlóan a Python-listák negatív indexeihez, az aktuális tengely végéhez viszonyított pozíciót jelzik. Ha a képeket középen 14 × 14 képpontos foltokra szeretné levágni, tegye a következőket:

my_slice = train_images[:, 7:-7, 7:-7]

2.2.7 Az adatkötegek fogalma

{35.o:} Általánosságban elmondható, hogy az első tengely (0-s tengely, mert az indexelés 0-tól kezdődik) a mélytanulás során használt összes adattenzorban a mintatengely lesz (ezt néha minta-dimenziónak is nevezik). Az MNIST példában a „minták” számjegyek képei.

Ezenkívül a mélytanulási modellek nem dolgoznak fel egyszerre egy teljes adatkészletet; hanem kis kötegekre bontják az adatokat. Konkrétan, íme egy köteg MNIST számjegyeinkből, 128-as kötegmérettel:

batch = train_images[:128]

És itt a következő adag:

batch = train_images[128:256]

És az n-edik adag:

n = 3
batch = train_images[128 * n:128 * (n + 1)]

Ha ilyen kötegtenzorra gondolunk, akkor az első tengelyt (0. tengely) kötegtengelynek vagy kötegdimenziónak nevezzük. Ez egy olyan kifejezés, amellyel gyakran találkozik a Keras és más mélytanulási könyvtárak használatakor.

2.2.8 Valós példák adattenzorokra

Tegyük konkrétabbá az adattenzorokat néhány példával, amelyek hasonlóak ahhoz, amivel később találkozni fog. A kezelni kívánt adatok szinte mindig a következő kategóriák valamelyikébe tartoznak:

2.2.9 Vektor adatok

Ez az egyik leggyakoribb eset. Egy ilyen adatkészletben minden egyes adatpont vektorként kódolható, és így egy adatköteg másodrendű tenzorként (vagyis vektortömbként) lesz kódolva, ahol az első tengely a minta tengelye és a második tengely a jellemzők tengelye. {36.o:}

Nézzünk két példát:

2.2.10 Idősor adatok vagy sorrendi adatok

Amikor az idő számít az adatokban (az időrendi sorrend értelmében), akkor célszerű egy explicit időtengellyel rendelkező harmadrendű tenzorban tárolni. Minden minta vektorok sorozataként (másodrendű tenzorként) kódolható, és így egy köteg adatot harmadrendű tenzorként kódolunk (lásd a 2.3. ábrát).

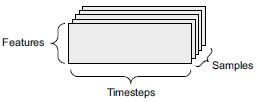
2.3. ábra Egy harmadrendű idősor adattenzor

Az időtengely megegyezés szerint mindig a második tengely (az 1-es index tengelye). Nézzünk néhány példát:

2.2.11 Képadatok

A képek általában három dimenzióval rendelkeznek: magasság, szélesség és színmélység. Bár a szürkeárnyalatos képeknek (mint az MNIST számjegyeink) csak egyetlen színcsatornájuk van, és így másodrendű tenzorokban tárolhatók, a képtenzorok a megegyezés szerint mindig harmadrendűek, a szürkeárnyalatos képekhez egydimenziós színcsatornával. Így egy 128 db 256 × 256 méretű szürkeárnyalatos képből álló köteg egy (128, 256, 256, 1) méretű tenzorban, egy 128 színes képből álló köteg pedig egy (128, 256, 256, 3) tenzorban tárolható (lásd a 2.4. ábrát).

2.4. ábra: Negyedrendű képadattenzor

Két konvenció létezik a képtenzorok alakjára: a channels-last konvenció (amely a TensorFlow-ban szabványos) és a channels-first konvenció (amely egyre inkább kegyvesztett). A channels-last konvenció a színmélység tengelyt a végére helyezi: (minták, magasság, szélesség, színmélység). Eközben a channels-first konvenció a színmélység tengelyét közvetlenül a kötegtengely után helyezi el: (minták, színmélység, magasság, szélesség). A channels-first konvencióval az előző példák (128, 1, 256, 256) és (128, 3, 256, 256) lesznek. A Keras API mindkét formátumot támogatja.

2.2.12 Videó adatok

A videoadatok azon kevés valós-életbeli adattípusok egyike, amelyekhez ötödrendű tenzorokra lesz szükség. A videó felfogható képkockák sorozataként, amelyek mindegyike színes kép. Mivel minden képkocka tárolható harmadrendű tenzorban (magasság, szélesség, színmélység), a képkockák sorozata egy negyedrendű tenzorban tárolható (képkockák, magasság, szélesség, színmélység), és így egy köteg különböző videó ötödrendű tenzorban tárolható (minták, képkockák, magasság, szélesség, színmélység).

Például egy 60 másodperces, 144 × 256 méretű YouTube-videó, amelyet másodpercenként 4 képkocka sebességgel vettek fel, 240 képkockát tartalmazna. Négy ilyen videoklipből álló köteg egy (4, 240, 144, 256, 3) méretű tenzorban kerül tárolásra. Ez összesen 106 168 320 érték! Ha a tenzor dtype értéke float32, akkor minden érték 32 biten lenne tárolva, így a tenzor 405 MB-ot jelentene. Súlyos! A valós életben talált videók sokkal könnyebbek, mert nem float32-ben tárolódnak, és általában nagy tényezővel tömörítik őket (például MPEG formátumban).

2.3 A neurális hálózatok fogaskerekei: Tenzorműveletek

Ahogyan bármely számítógépes program végső soron bináris bemeneteken végrehajtott bináris műveletek kis halmazára redukálható (ÉS, VAGY, NOR és így tovább), a mély neurális hálózatok által megtanult összes transzformáció egy maroknyi tenzorműveletre (vagy tenzor függvényre) redukálható, amiket numerikus adatok tenzoraira alkalmazunk. Például lehetőség van tenzorok összeadására, tenzorok szorzására és így tovább.

Kezdeti példánkban a modellünket úgy építettük fel, hogy Dense (sűrű) rétegeket raktunk egymásra. A Keras réteg példánya így néz ki:

keras.layers.Dense(512, activation="relu")

Ez a réteg függvényként értelmezhető, amely bemenetként egy mátrixot vesz, és egy másik mátrixot ad vissza – a bemeneti tenzor új reprezentációját. Pontosabban, a függvény a következő (ahol W egy mátrix és b egy vektor, mindkét réteg attribútuma):

output = relu(dot(input, W) + b)

Csomagoljuk ki ezt. Itt három tenzorműveletünk van:

MEGJEGYZÉS

Bár ez a rész teljes egészében a lineáris algebrai kifejezésekkel foglalkozik, itt nem talál matematikai jelöléseket. Azt tapasztaltam, hogy a matematikai fogalmakat könnyebben el tudják sajátítani a matematikai háttérrel nem rendelkező programozók, ha matematikai egyenletek helyett rövid Python-részletként fejezik ki őket. Tehát mindvégig a NumPy és a TensorFlow kódot fogjuk használni.

2.3.1 Elemenkénti műveletek

A relu művelet és az összeadás elemenkénti műveletek: olyan műveletek, amelyek függetlenül kerülnek alkalmazásra a vizsgált tenzorok minden egyes bejegyzésére. Ez azt jelenti, hogy ezek a műveletek nagymértékben alkalmasak masszívan párhuzamos megvalósításokra (vektorizált implementációk, ez a kifejezés az 1970–90-es időszak vektorprocesszoros szuperszámítógép-architektúrájából származik). Ha naiv Python-megvalósítást szeretne írni egy elemenkénti művelethez, akkor for ciklust használjon, mint az elemenkénti relu művelet naiv megvalósításában:

def naive_relu(x):
    assert len(x.shape) == 2      #<--- x egy másodrendű NumPy tenzor.
    x = x.copy()                  #<--- Kerüljük a bemeneti tenzor felülírását.
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] = max(x[i, j], 0)
    return x

Ugyanezt megteheti az összeadáshoz:

def naive_add(x, y):
    assert len(x.shape) == 2      #<--- x és y másodrendű NumPy tenzor.
    assert x.shape == y.shape
    x = x.copy()                  #<--- Kerüljük a bemeneti tenzor felülírását.
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] += y[i, j]
    return x

Ugyanezen az elven elvégezheti az elemenkénti szorzást, kivonást és így tovább. A gyakorlatban a NumPy tömbök kezelésekor ezek a műveletek jól optimalizált beépített NumPy függvényekként érhetők el, amelyek maguk delegálják a nehéz terheket egy Basic Linear Algebra Subprograms (BLAS) megvalósításra. A BLAS alacsony szintű, nagyon párhuzamos, hatékony tenzormanipulációs rutinok, amelyeket jellemzően Fortran vagy C nyelven valósítanak meg. Tehát a NumPy-ben képes elvégezni a következő elemenkénti műveletet, és gyorsan fog működni:

import numpy as np
z = x + y               #<--- elemszintű összeadás
z = np.maximum(z, 0.)   #<--- elemszintű relu

Állapítsuk meg a tényleges időkülönbséget:

import time

x = np.random.random((20, 100))
y = np.random.random((20, 100))

t0 = time.time()
for _ in range(1000):
    z = x + y
    z = np.maximum(z, 0.)
print("Took: {0:.2f} s".format(time.time() - t0))

Ez csak 0,02 másodpercet vesz igénybe. Miközben a naiv verzió meglepő 2,45 másodpercet kíván:

t0 = time.time()
for _ in range(1000):
    z = naive_add(x, y)
    z = naive_relu(z)
print("Took: {0:.2f} s".format(time.time() - t0))

Hasonlóképpen, ha TensorFlow kódot futtat egy GPU-n, az elemenkénti műveletek végrehajtása teljesen vektorizált CUDA-megvalósításokon keresztül történik, amelyek a legjobban tudják kihasználni a rendkívül párhuzamos GPU-chip architektúrát:

2.3.2 Kiterjesztés (broadcasting)

A naive_add korábbi naiv megvalósítása csak az azonos alakú másodrendű tenzorok összeadását támogatja. De a korábban bemutatott Dense rétegben összeadtunk egy másodrendű tenzort egy vektorral. Mi történik az összeadással, ha a két összeadandó tenzor alakja különbözik?

Ha lehetséges, és ha nincs kétértelműség, a kisebb tenzort kiterjesztik, hogy megfeleljen a nagyobb tenzor alakjának. A kiterjesztés két lépésből áll:

  1. Tengelyek (úgynevezett broadcast tengelyek) adódnak hozzá a kisebb tenzorhoz, hogy megfeleljenek a nagyobb tenzor ndim-jének.
  2. A kisebb tenzor megismétlődik ezen új tengelyek mentén, hogy megfeleljen a nagyobb tenzor teljes alakjának.

Nézzünk egy konkrét példát. Tekintsük a (32, 10) méretű X-et és a (10,) méretű y-t:

import numpy as np
X = np.random.random((32, 10))  #<--- X egy (32, 10) méretű véletlenszerű mátrix.
y = np.random.random((10,))     #<--- y egy (10,) méretű véletlenszerű vektor.

Először egy üres első tengelyt adunk az y-hoz, amelynek mérete így (1, 10)-re változik:

y = np.expand_dims(y, axis=0)   #<--- Az y mérete most (1, 10).

Ezután y-t 32-szer megismételjük az új tengely mentén, így a (32, 10) méretű Y tenzort kapjuk, ahol Y[i, :] == y for i in range(0, 32):

Y = np.concatenate([y] * 32, axis=0)    #<--- Megismételjük az y-t 32-szer a 0 tengely mentén,
                                        #     hogy megkapjuk Y-t, amelynek mérete (32, 10).

Ezen a ponton folytathatjuk az X és Y összeadását, mert azonos alakúak.

A megvalósítás szempontjából nem jön létre új másodrendű tenzor, mert az rettenetesen pazarló lenne. Az ismétlési művelet teljesen virtuális: algoritmikus szinten történik, nem pedig memória szinten. De ha azt gondoljuk, hogy a vektor 10-szer ismétlődik egy új tengely mellett, az hasznos mentális modell. Így nézne ki egy naiv megvalósítás:

def naive_add_matrix_and_vector(x, y):
    assert len(x.shape) == 2            #<--- x egy másodrendű NumPy tenzor.
    assert len(y.shape) == 1            #<--- y egy NumPy vektor.
    assert x.shape[1] == y.shape[0]
    x = x.copy()                        #<--- Kerüljük a bemeneti tenzor felülírását.
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] += y[j]
    return x

A kiterjesztéssel általában elemenkénti műveletek hajthatók végre, amelyek két bemeneti tenzort vesznek át, ha az egyik tenzor mérete (a, b, … n, n + 1, … m), és a másik mérete pedig (n, n + 1, … m). A kiterjesztés ezután automatikusan megtörténik az a-tól n-1 tengelyeken.

A következő példa az elemenkénti maximum műveletet két különböző alakú/méretű tenzorra alkalmazza kiterjesztésen/sugárzáson keresztül:

import numpy as np
x = np.random.random((64, 3, 32, 10))   #<--- x egy véletlenszerű tenzor, amelynek mérete (64, 3, 32, 10).
y = np.random.random((32, 10))          #<--- x egy véletlenszerű tenzor, amelynek mérete (32, 10).
z = np.maximum(x, y)                    #<--- A z kimenet mérete (64, 3, 32, 10), mint az x-é.

2.3.3 Tenzor szorzat

A tenzorszorzat vagy pontszorzat (nem tévesztendő össze az elemi szorzattal, a * operátorral) az egyik leggyakoribb, leghasznosabb tenzorművelet.

A NumPy-ban a tenzorszorzat az np.dot függvény segítségével történik (mivel a tenzorszorzat matematikai jelölése általában pont):

x = np.random.random((32,))
y = np.random.random((32,))
z = np.dot(x, y)

A matematikai felírásban a műveletet egy ponttal (•) jelöljük:

z = x • y

Matematikailag mit csinál a pontművelet? Kezdjük két vektor, x és y pontszorzatával. A következőképpen kerül kiszámításra:

def naive_vector_dot(x, y):
    assert len(x.shape) == 1    #<--- x és y NumPy vektor
    assert len(y.shape) == 1    #
    assert x.shape[0] == y.shape[0]
    z = 0.
    for i in range(x.shape[0]):
        z += x[i] * y[i]
    return z

Biztosan észrevette, hogy a két vektor közötti pontszorzat skalár, és csak az azonos elemszámú vektorok kompatibilisek a pontszorzattal.

Használhatja az x mátrix és egy y vektor közötti pontszorzatot is, amely egy olyan vektort ad vissza, ahol az együtthatók az y és az x sorai közötti pontszorzatok. A következőképpen valósíthatjuk meg: {42.o:}

def naive_matrix_vector_dot(x, y):
    assert len(x.shape) == 2          #<--- x egy NumPy mátrix
    assert len(y.shape) == 1          #<--- y wgy NumPy vektor
    assert x.shape[1] == y.shape[0]   #<--- x első dimenziójának meg kell egyeznie y 0. dimenziójával!
    z = np.zeros(x.shape[0])          #<--- Ez a művelet egy nullvektort ad vissza, amelynek mérete megegyezik y-éval.
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            z[i] += x[i, j] * y[j]
    return z

Használhatja megint azt a korábban írt kódot, amely kiemeli a mátrix-vektor-szorzat és a vektor-szorzat közötti kapcsolatot:

def naive_matrix_vector_dot(x, y):
    z = np.zeros(x.shape[0])
    for i in range(x.shape[0]):
        z[i] = naive_vector_dot(x[i, :], y)
    return z

Jegyezze meg, hogy amint a két tenzor egyikének ndim-je nagyobb, mint 1, akkor a dot többé nem szimmetrikus, vagyis a dot(x, y) nem ugyanaz, mint a dot(y, x).

Természetesen a pontszorzat tetszőleges számú tengellyel rendelkező tenzorokra általánosít. A leggyakoribb alkalmazás a két mátrix közötti pontszorzat lehet. Az x és y mátrix (dot(x, y)) pontszorzatát akkor és csak akkor képezhetjük, ha x.shape[1] == y.shape[0]. Az eredmény egy (x.shape[0], y.shape[1]) alakú mátrix , ahol az együtthatók az x sorai és az y oszlopai közötti vektorszorzatok. Íme a naiv megvalósítás:

def naive_matrix_dot(x, y):
    assert len(x.shape) == 2                #<--- x és y NumPy mátrixok.
    assert len(y.shape) == 2                #
    assert x.shape[1] == y.shape[0]         #<--- x első dimenziójának meg kell egyeznie y 0. dimenziójával!
    z = np.zeros((x.shape[0], y.shape[1]))  #<--- Ez a művelet egy meghatározott alakú nullmátrixot ad vissza.
    for i in range(x.shape[0]):             #<--- Az x sorai felett iterálunk...
        for j in range(y.shape[1]):         #<--- ... és y oszlopai fölött is.
            row_x = x[i, :]
            column_y = y[:, j]
            z[i, j] = naive_vector_dot(row_x, column_y)
    return z

A pontszorzat alak-kompatibilitásának megértésében segít a bemeneti és kimeneti tenzorok 2.5. ábrán látható módon csatlakoztatott megjelenítése.

Az ábrán x, y és z értékét téglalapként (szó szerint együttható-dobozokként) ábrázoltuk. Mivel x sorainak és y oszlopainak azonos méretűnek kell lenniük, ebből az következik, hogy x szélességének meg kell egyeznie y magasságával. Ha új gépi tanulási algoritmusokat fejleszt, valószínűleg gyakran fog ilyen diagramokat rajzolni.

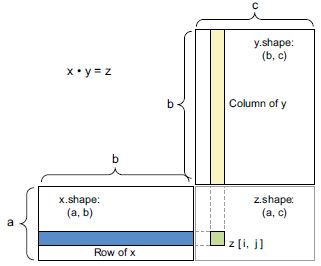
2.5. ábra: Mátrix pontszorzat dobozdiagram

Általánosságban elmondható, hogy pontszorzatot a több-dimenziós tenzorok között kaphat, ugyanazokat az alakkompatibilitási szabályokat követve, mint a 2D esetnél korábban vázoltuk:

(a, b, c, d) • (d,) → (a, b, c)
(a, b, c, d) • (d, e) → (a, b, c, e)

És így tovább.

2.3.4 Tenzor átalakítás (reshape)

A tenzorműveletek harmadik típusa, amely a megértéshez elengedhetetlen, a tenzor átalakítás. Bár az első neurális hálózati példánkban nem használtuk a Dense rétegekben, akkor használtuk, amikor előfeldolgoztuk a számadatokat, mielőtt betápláltuk volna őket a modellünkbe:

train_images = train_images.reshape((60000, 28 * 28))

A tenzor átformálása azt jelenti, hogy sorait és oszlopait átrendezzük, hogy megfeleljenek a célalakzatnak. Természetesen az átformált tenzornak ugyanannyi együtthatója van, mint a kezdeti tenzornak. Az átformálást legjobban egyszerű példákon keresztül érthetjük meg:

>>> x = np.array([[0., 1.],
                  [2., 3.],
                  [4., 5.]])
>>> x.shape
(3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[ 0.],
       [ 1.],
       [ 2.],
       [ 3.],
       [ 4.],
       [ 5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
       [ 3., 4., 5.]])

Az átalakítás speciális esete, amellyel gyakran találkozunk, a transzponálás. Egy mátrix transzponálása azt jelenti, hogy felcseréljük sorait és oszlopait, így x[i, :]-ből x[:, i] lesz:

>>> x = np.zeros((300, 20))   #<--- Létrehoz egy (300, 20) alakú nullmátrixot.
>>> x = np.transpose(x)
>>> x.shape
(20, 300)

2.3.5 Tenzorműveletek geometriai értelmezése

Mivel a tenzorműveletekkel manipulált tenzorok tartalma valamilyen geometriai térben lévő pontok koordinátáiként értelmezhető, minden tenzorműveletnek van geometriai értelmezése. Vegyük például az összeadást. Kezdjük a következő vektorral:

A = [0.5, 1]

Ez egy pont egy 2D-s térben (lásd a 2.6. ábrát). Gyakori, hogy egy vektort nyílként ábrázolnak, amely összeköti az origót a ponttal, amint az a 2.7. ábrán látható.

2.6. ábra: Egy pont a 2D-s térben

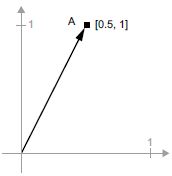
2.7. ábra: Egy pont a 2D-s térben nyílként ábrázolva

Tekintsünk egy új pontot, B = [1, 0.25], amelyet hozzáadunk az előzőhöz. Ez geometriailag a vektornyilak láncolásával történik, ahol a kapott hely az előző két vektor összegét reprezentáló vektor (lásd a 2.8. ábrát). Amint látható, a B vektor hozzáadása az A vektorhoz azt jelenti, hogy az A pont egy új helyre másolódik, amelynek távolságát és irányát az eredeti A ponttól a B vektor határozza meg. Ha ugyanazt a vektorösszeadást alkalmazzuk egy pontcsoportra (egy „objektum”-ra) a síkban, akkor a teljes objektum másolatát készítenénk el egy új helyen (lásd a 2.9. ábrát). A tenzorösszeadás tehát azt a műveletet jelenti, amikor egy objektumot egy bizonyos mértékben egy bizonyos irányba eltolnak (az objektumot torzítás nélkül mozgatják).

2.8. ábra: Két vektor összegének geometriai értelmezése

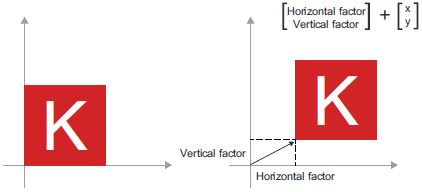
2.9. ábra: 2D eltolás vektorösszeadásként

Általánosságban elmondható, hogy az olyan elemi geometriai műveletek, mint az eltolás, elforgatás, átméretezés, döntés stb., tenzorműveletekként fejezhetők ki. Íme néhány példa:

2.10. ábra: 2D forgatás (az óramutató járásával ellentétes irányba) pontszorzatként

2.11. ábra: 2D átméretezés pontszorzatként

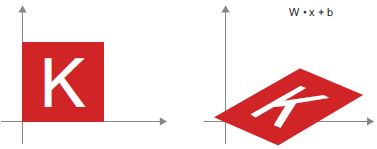
2.12 ábra: Affin transzformáció a síkban

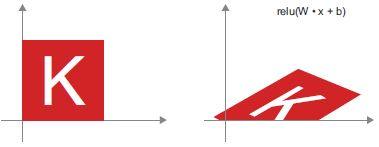
2.13 ábra: Affin transzformáció, majd relu aktiválás

2.3.6 A mélytanulás geometriai értelmezése

Most tanulta meg, hogy a neurális hálózatok teljes egészében tenzorműveletek láncaiból állnak, és hogy ezek a tenzorműveletek a bemeneti adatok egyszerű geometriai transzformációi. Ebből az következik, hogy a neurális hálózatot egy nagyon összetett geometriai transzformációként értelmezheti egy nagy dimenziós térben, amelyet egyszerű lépések sorozatával valósítanak meg.

3D-ben a következő mentális kép hasznos lehet. Képzeljen el két színes papírlapot: egy pirosat és egy kéket. Tegye egyiket a másikra. Most gyűrje össze őket egy kis golyóvá. Ez a gyűrött papírgolyó a bemeneti adat, és minden papírlap egy osztályozási probléma adatosztálya. Egy neurális hálózatnak az a célja, hogy kitalálja a papírgömb transzformációját, amely szétszedi, így a két osztály ismét tisztán elválaszthatóvá válik (lásd a 2.14. ábrát). A mélytanulással ez a 3D-s tér egyszerű átalakításainak sorozataként valósulna meg, például azokkal, amelyeket ujjaival, egy-egy mozdulattal tudna alkalmazni a papírgolyóra.

2.14. ábra: Bonyolult adathalmaz kibontása

A papírgolyók kibontása a gépi tanulás lényege: az összetett, erősen hajtogatott adatelosztók ügyes reprezentációinak megtalálása nagy dimenziójú terekben (az elosztó egy folytonos felület, akárcsak a mi gyűrött papírlapunk). Ezen a ponton elég jó intuícióval kell rendelkezned, hogy miért jeleskedik ebben a mélytanulás: ez azt a megközelítést követi, hogy egy bonyolult geometriai transzformációt fokozatosan lebontanak elemiek hosszú láncára, ami nagyjából az a stratégia, amelyet az ember követne a papírgolyó kibontására. A mélyhálózat minden rétege olyan transzformációt alkalmaz, amely egy kicsit szétválasztja az adatokat, és a rétegek mély verme rendkívül bonyolult szétválasztási folyamatot tesz lehetővé. {48.o:}

2.4 A neurális hálózatok motorja: Gradiens alapú optimalizálás

Ahogy az előző részben láthatta, az első modellpéldánkból származó minden egyes neurális réteg a következőképpen alakítja át bemeneti adatait:

output = relu(dot(input, W) + b)

Ebben a kifejezésben W és b tenzorok, amelyek a réteg attribútumai. Ezeket a réteg súlyainak vagy betanítható paramétereinek (a kernel és a bias ‘torzítás’ attribútumainak) nevezik. Ezek a súlyok azokat az információkat tartalmazzák, amelyeket a modell a képzési adatok expozíciójából tanul meg.

Kezdetben ezek a súlymátrixok kis véletlenszerű értékekkel vannak feltöltve (ezt a lépést véletlenszerű inicializálásnak nevezik). Természetesen nincs okunk arra számítani, hogy a relu(dot(input, W) + b), amikor W és b véletlenszerű, bármilyen hasznos reprezentációt ad. Az eredményül kapott reprezentációk értelmetlenek – de kiindulópontot jelentenek. A következő lépés a súlyok fokozatos, visszacsatolási jel alapján történő módosítása. Ez a fokozatos alkalmazkodás, amelyet képzésnek is neveznek, az a tanulás, amelyről az egész gépi tanulás szól.

Ez az úgynevezett képzési hurkon belül történik, amely a következőképpen működik. Ismételje meg ezeket a lépéseket egy hurokban, amíg a veszteség kellően kevésnek tűnik:

  1. Rajzoljon egy köteget tanítási mintákból, x és a megfelelő célokból, y_true.
  2. Futtassa a modellt x-en (ez a lépés, amelyet előrelépésnek neveznek), hogy megkapja az y_pred előrejelzéseket.
  3. Számítsa ki a modell veszteségét a kötegben, az y_pred és az y_true közötti eltérés mértékét.
  4. Frissítse a modell összes súlyát oly módon, hogy kissé csökkentse a tétel veszteségét.

Végül egy olyan modellt kap, amely nagyon alacsony veszteséggel rendelkezik a képzési adatokban: alacsony az eltérés az előrejelzések (y_pred) és a várható célok (y_true) között. A modell „megtanulta” bemeneteit a helyes célokra leképezni. Messziről varázslatnak tűnhet, de ha elemi lépésekre redukáljuk, egyszerűnek bizonyul.

Az 1. lépés elég egyszerűnek hangzik – csak I/O kód. A 2. és 3. lépés csupán néhány tenzorművelet alkalmazása, így ezeket a lépéseket pusztán az előző részben tanultak alapján hajthatja végre. A nehéz rész a 4. lépés: a modell súlyainak frissítése. A modellben szereplő egyéni súlyegyüttható alapján hogyan lehet kiszámítani, hogy az együtthatót növelni vagy csökkenteni kell-e, és mennyivel?

Az egyik naiv megoldás az lenne, ha a modellben az összes súlyt rögzítenénk, kivéve az egy skaláris együtthatót, és ennek az együtthatónak különböző értékekkel próbálkoznánk. Tegyük fel, hogy az együttható kezdeti értéke 0,3. Egy adatköteg továbbadása után a köteg modelljének vesztesége 0,5. Ha az együttható értékét 0,35-re változtatja, és megismétli az előrelépést, a veszteség 0,6-ra nő. De ha az együtthatót 0,25-re csökkenti, a veszteség 0,4-re csökken. Ebben az esetben úgy tűnik, hogy az együttható –0,05-tel történő frissítése hozzájárulna a veszteség minimalizálásához. Ezt meg kell ismételni a modell összes együtthatójára.

De egy ilyen megközelítés rettenetesen hatástalan lenne, mert minden egyes együtthatóhoz (amelyből sok van, általában több ezer, néha akár millió is) két előrepasszt (amelyek költségesek) kellene kiszámítani. Szerencsére van egy sokkal jobb megközelítés: a gradiens ereszkedés.

A gradiens ereszkedés az az optimalizálási technika, amely a modern neurális hálózatokat működteti. Íme a lényeg. A modelljeinkben használt összes függvény (mint például a dot vagy a +) simán és folytonosan átalakítja a bemenetét: ha például z = x + y-t nézzük, y-ben egy kis változás csak kis változást eredményez z-ben, és ha ismeri y változásának irányát, akkor következtetni tud z változásának irányára. Matematikailag azt mondanád, hogy ezek a függvények differenciálhatók. Ha összeláncolja az ilyen függvényeket, a kapott nagyobb függvény továbbra is differenciálható. Ez különösen vonatkozik arra a függvényre, amely a modell együtthatóit leképezi a modell veszteségére egy adatkötegben: a modell együtthatóinak kis változása kis, előre látható változást eredményez a veszteség értékében. Ez lehetővé teszi, hogy a gradiensnek nevezett matematikai operátort leírja, hogyan változik a veszteség, amikor a modell együtthatóit különböző irányokba mozgatja. Ha kiszámítja ezt a gradienst, akkor használhatja az együtthatók mozgatására (egy frissítésben egyszerre, nem pedig egyenként) a veszteséget csökkentő irányba.

Ha már tudja, mit jelent a differenciálhatóság és mi a gradiens, akkor ugorjon a 2.4.3. szakaszra. Ellenkező esetben a következő két rész segít megérteni ezeket a fogalmakat.

2.4.1 Mi az a derivált?

Tekintsünk egy f(x) = y folytonos, sima függvényt, amely egy x számot képez le egy új y számra. Példaként használhatjuk a 2.15. ábra függvényét.

2.15. ábra: Folyamatos, sima függvény

Mivel a függvény folytonos, az x kis változása csak kis változást eredményezhet y-ban – ez a folytonosság mögött meghúzódó intuíció. Tegyük fel, hogy növeli x-et egy kis tényezővel, epszilon_x-szel: ez egy kis epsilon_y változást eredményez y-ban, amint azt a 2.16. ábra mutatja.

2.16. ábra: Folyamatos függvény esetén az x kis változása y kis változását eredményezi.

Továbbá, mivel a függvény sima (a görbéjének nincsenek hirtelen szögletei), amikor az epsilon_x elég kicsi, egy bizonyos p pont körül, akkor közelíthető az f függvény az a meredekség lineáris függvényeként, így az epsilon_y egy a * epszilon_x érték lesz:

f(x + epsilon_x) = y + a * epsilon_x

Nyilvánvaló, hogy ez a lineáris közelítés csak akkor érvényes, ha x elég közel van p-hez. Az a meredekséget nevezzük f p pontban vett deriváltjának. Ha a negatív, az azt jelenti, hogy az x kismértékű növekedése p körül az f(x) csökkenését eredményezi (ahogyan a 2.17. ábrán látható), és ha a pozitív, akkor x kis növekedése f(x) növekedését eredményezi. Továbbá az a abszolút értéke (a derivált nagysága) megmutatja, hogy ez a növekedés vagy csökkenés milyen gyorsan fog bekövetkezni.

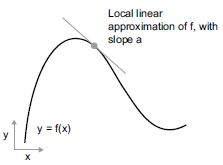
2.17. ábra: Az f deriváltja p-ben

Minden f(x) differenciálható függvényre (a differenciálható azt jelenti, hogy „lehet deriválni”: például a sima, folytonos függvényeket lehet deriválni) létezik egy f'(x) derivált függvény, amely leképezi x értékeit az f helyi lineáris közelítésének ezen pontokban vett meredekségére. Például cos(x) deriváltja -sin(x), f(x) = a * x deriváltja f'(x) = a, és így tovább.

A függvények deriválása nagyon hatékony eszköz az optimalizáláshoz, az olyan x értékek megtalálásához, amelyek minimalizálják f(x) értékét. Ha megpróbáljuk az x-et egy epszilon_x tényezővel módosítani azért, hogy minimalizáljuk f(x) értékét, és ismerjük f deriváltját, akkor a munka kész: a derivált tökéletesen leírja, hogyan alakul f(x) az x megváltoztatásakor. Ha f(x) értékét szeretnénk csökkenteni, akkor x-et csak egy kicsit kell a deriválttal ellentétes irányba elmozdítanunk. {51.o:}

2.4.2 Tenzorművelet deriváltja: A gradiens

A függvény, amit fentebb néztünk, egy x skalárértéket egy másik y skalárértékké alakított át: ezt görbeként 2D síkban tudtuk ábrázolni. Most képzeljünk el egy függvényt, amely a skalárok sorát (x, y) z skalárértékké alakítja: ez egy vektorművelet lenne. 2D felületként tudnánk ábrázolni a 3D térben (x, y, z koordinátákkal indexelve). Hasonlóképpen elképzelhetünk olyan függvényeket, amelyek mátrixokat fogadnak bemenetként; olyan függvényeket, amelyek bemenetként harmadrendű tenzorokat vesznek át, stb.

A deriválás fogalma bármely ilyen függvényre alkalmazható, amennyiben az általuk leírt felületek folytonosak és simák. A tenzorművelet (vagy tenzorfüggvény) deriváltját gradiensnek nevezzük. A gradiens csak a derivált fogalmának általánosítása olyan függvényekre, amelyek tenzorokat fogadnak bemenetként. Emlékszel, hogy skalárfüggvény esetén a derivált a függvény görbéjének lokális meredekségét reprezentálja? Ugyanígy a tenzorfüggvény gradiense a függvény által leírt többdimenziós felület görbületét reprezentálja. Ez írja le, hogy a függvény kimenete hogyan változik, ha a bemeneti paraméterei változnak.

Nézzünk egy gépi tanuláson alapuló példát. Gondoljunk ezekre:

A W segítségével tudjuk kiszámítani az y_pred kijelölt célt, majd kiszámítani az y_pred kijelölt cél és az y_true cél közötti veszteséget vagy eltérést:

y_pred = dot(W, x)                  #<--- A modellsúlyokat (W) használjuk az x előrejelzésére.
loss_value = loss(y_pred, y_true)   #<--- Megbecsüljük, milyen messze volt az előrejelzés.

Most gradienseket szeretnénk használni, hogy kitaláljuk, hogyan lehet úgy frissíteni W-t, hogy a loss_value kisebb legyen. Hogyan csináljuk?

A rögzített x és y_true bemenetek mellett az előző műveletek értelmezhetők a W értékeinek (a modell súlyainak) a veszteségértékekre való leképezéseként:

loss_value = f(W)       #<--- f írja le azt a görbét (vagy többdimenziós felületet), amelyet a veszteségértékek alkotnak, ha W változik.

Tegyük fel, hogy W jelenlegi értéke W0. Ekkor f deriváltja a W0 pontban egy tenzor grad(loss_value, W0), ugyanolyan alakú, mint W, ahol minden együttható grad(loss_value, W0)[i, j] jelzi a loss_value változásának irányát és nagyságát, amely a W0[i, j] módosításakor figyelhető meg. Ez a tenzor grad(loss_value, W0) az f(W) = loss_value függvény gradiense W0-ban, más néven „a loss_value W-re vonatkozó gradiense W0 körül”. {52.o:}

Parciális deriváltak

A grad(f(W), W) tenzorművelet (amely bemenetként egy W mátrixot fogad) skaláris függvények kombinációjaként fejezhető ki, grad_ij(f(W), w_ij), amelyek mindegyike a loss_value = f(W) deriváltját adja vissza a W W[i, j] együtthatójára vonatkozóan, feltételezve, hogy az összes többi együttható állandó. A grad_ij-t f W[i, j]-re vonatkozó parciális deriváltjának nevezzük.

Konkrétan mit jelent a grad(los_value, W0)? Korábban láttad, hogy egyetlen együttható f(x) függvényének deriváltja az f görbéjének meredekségeként értelmezhető. Hasonlóképpen, a grad(loss_value, W0) úgy értelmezhető, mint a tenzor, amely leírja a loss_value = f(W) legmeredekebb emelkedési irányát W0 körül, valamint az emelkedés meredekségét. Mindegyik parciális derivált f meredekségét írja le egy adott irányban.

Emiatt nagyjából ugyanúgy, mint az f(x) függvénynél, csökkenteni tudjuk az f(x) értékét, ha x-et a deriválttal ellentétes irányban egy kicsit elmozdítjuk egy f(W) tenzorfüggvény segítségével csökkenthetjük a loss_value = f(W) értékét, ha W-t a gradienssel ellentétes irányba mozdítjuk: például W1 = W0 - step * grad(f(W0), W0) (ahol a step egy kis méretező tényező). Ez azt jelenti, hogy az f legmeredekebb emelkedési irányával ellentétes irányba haladunk, ami intuitív módon lejjebb visz a görbén. Vegyük észre, hogy a step skálázási tényezőre azért van szükség, mert a grad(loss_value, W0) csak akkor közelíti meg a görbületet, ha közel vagyunk a W0-hoz, tehát nem szeretnénk túl messzire kerülni a W0-tól.

2.4.3 Sztochasztikus gradiens ereszkedés (SGD)

Adott egy differenciálható függvény; elméletileg lehetséges analitikusan megtalálni a minimumát: köztudott, hogy egy függvény minimuma az a pont, ahol a derivált értéke 0, tehát mindössze annyit kell tenni, hogy meg kell találni azokat a pontokat, ahol a derivált 0-vá válik, és ellenőrizni kell, hogy ezek közül a pontok közül a függvénynek hol van a legkisebb értéke.

Neurális hálózatra alkalmazva ez azt jelenti, hogy analitikusan megtaláljuk a súlyértékek azon kombinációját, amely a lehető legkisebb veszteségfüggvényt eredményezi. Ez a grad(f(W), W) = 0 egyenlet W-re történő megoldásával tehető meg. Ez egy N változóból álló polinomiális egyenlet, ahol N a modellben szereplő együtthatók száma. Bár lehetséges lenne egy ilyen egyenletet megoldani N = 2 vagy N = 3 esetén, ez megoldhatatlan valódi neurális hálózatok esetében, ahol a paraméterek száma soha nem kevesebb néhány ezernél, és gyakran több tízmillió is lehet.

Ehelyett használhatjuk a szakasz elején felvázolt négylépéses algoritmust: apránként módosítsa a paramétereket egy véletlenszerű adatköteg aktuális veszteségi értéke alapján. Mivel differenciálható függvénnyel van dolgunk, ki tudjuk számítani annak gradiensét, ami hatékony módot ad a 4. lépés végrehajtására. Ha a súlyokat a gradienssel ellentétes irányba frissítjük, a veszteség minden alkalommal valamivel kisebb lesz:

  1. Húzzunk ki egy köteget a tanítási mintákból, x-et, és a megfelelő célokat, y_true-t.
  2. Futtassuk a modellt x-en, hogy előrejelzéseket kapjunk, y_pred-et (ezt hívják előrelépésnek).
  3. Számítsuk ki a modell veszteségét a kötegben, az y_pred és az y_true közötti eltérés mértékét.
  4. Számítsuk ki a veszteség gradiensét a modell paraméterei alapján (ezt nevezzük visszafelé haladásnak).
  5. Mozgassuk a paramétereket egy kicsit a gradienssel ellentétes irányba – például W -= learning_rate * gradient –, így egy kicsit csökkentjük a köteg veszteségét. A tanulási sebesség (itt a learning rate) a gradiens ereszkedési folyamat „sebességét” módosító skaláris tényező lenne.

Elég könnyű! Amit az imént leírtunk, az úgynevezett mini-köteg sztochasztikus gradiens ereszkedés (mini-batch SGD). A sztochasztikus kifejezés arra a tényre utal, hogy minden adatköteget véletlenszerűen “húzunk ki” (a sztochasztikus a véletlen tudományos szinonimája). A 2.18. ábra szemlélteti, hogy mi történik 1D-ben, amikor a modellnek csak egy paramétere van, és csak egy betanítási mintája van.

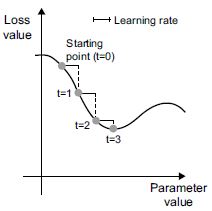
2.18 ábra: SGD lefelé egy 1D veszteségi görbén (egy tanulható paraméter)

Amint látja, intuitív módon fontos ésszerű értéket választani a tanulási arány (learning_rate) tényezőhöz. Ha túl kicsi, a görbén lefelé ereszkedés sok iterációt igényel, és megrekedhet a helyi minimumban. Ha a learning_rate túl nagy, a frissítések végül teljesen véletlenszerű helyekre juttathatnak el minket a görbén.

Vegye észre, hogy a mini kötegelt SGD-algoritmus egyik változata egyetlen mintát húz és céloz mindegyik iterációnál ahelyett, hogy egy köteg adatot húzna. Ez valódi SGD lenne (szemben a mini-batch SGD-vel). Alternatív megoldásként, ha az ellenkező végletbe csapnánk át, minden lépést lefuttatnánk az összes elérhető adaton, amit kötegelt gradiens ereszkedésnek neveznek. Minden frissítés pontosabb, de sokkal drágább lenne. A két véglet közötti hatékony kompromisszum az észszerű méretű mini-kötegek használata.

Bár a 2.18. ábra a gradiens ereszkedést egy 1D paramétertérben szemlélteti, a gyakorlatban a gradiens ereszkedést sok dimenziójú terekben fogjuk használni: egy neurális hálózatban minden súlyegyüttható szabad dimenzió a térben, és lehet több tízezer vagy akár millió is belőlük. A veszteségfelületekkel kapcsolatos intuíció kialakítása érdekében a 2D veszteségfelület mentén történő gradiens ereszkedést is megjeleníthetjük, amint az a 2.19. ábrán látható. De nem lehet elképzelni, hogyan néz ki egy neurális hálózat képzésének tényleges folyamata – nem tudunk ábrázolni egy 1 000 000 dimenziós teret úgy, hogy az az emberek számára is értelmes legyen. Emiatt jó észben tartani, hogy a kevés dimenziós ábrázolásokon keresztül kifejlesztett intuíciók nem mindig pontosak a gyakorlatban. Ez történelmileg problémák forrása volt a mélytanulási kutatás világában. {54.o:}

2.19. ábra: Gradiens ereszkedés egy 2D veszteségfelületen (két tanulható paraméternél)

Ezenkívül az SGD-nek több változata is létezik, amelyek abban különböznek, hogy a következő súlyfrissítés kiszámításakor figyelembe veszik a korábbi súlyfrissítéseket, ahelyett, hogy csak a gradiensek aktuális értékét néznék. Ott van például az SGD with momentum, valamint az Adagrad, az RMSprop és még sokan mások. Az ilyen változatokat optimalizálási módszereknek vagy optimalizálóknak nevezzük. Különösen a momentum (lendület) fogalma érdemel figyelmet, amelyet sok ilyen változatban használnak. A momentum két SGD-vel kapcsolatos gonddal foglalkozik: a konvergencia sebességével és a helyi minimumokkal. Tekintsük a 2.20 ábrát, amely a veszteség görbéjét mutatja egy modellparaméter függvényében.

2.20. ábra: Egy lokális minimum és egy globális minimum

Mint látható, egy bizonyos paraméterérték körül van egy lokális minimum: ezen a ponton balra mozgatva a veszteség növekedne, de a jobbra mozgásnál is. Ha a vizsgált paramétert SGD-n keresztül optimalizálnák kis tanulási sebességgel, akkor az optimalizálási folyamat megakadhat a lokális minimumnál, ahelyett, hogy a globális minimum felé haladna. Az ilyen problémákat elkerülheti, ha lendületet használ, amely a fizikából merít ihletet. Hasznos mentális kép, ha az optimalizálási folyamatot úgy tekintjük, mint egy kis golyót, amely a veszteséggörbén gördül lefelé. Ha van elég lendülete, akkor a labda nem akad el egy mélyedésben, és a globális minimumra kerül. A lendületet úgy valósítják meg, hogy a golyómozgást mindegyik lépésben módosítják, nem csak az aktuális meredekség értéke (aktuális gyorsulás), hanem az aktuális sebesség (a múltbeli gyorsulás eredménye) alapján is. Ez a gyakorlatban azt jelenti, hogy a w paramétert nem csak az aktuális gradiensérték alapján kell frissíteni, hanem az előző paraméterfrissítés alapján is, mint például ebben a naiv megvalósításban:

past_velocity = 0.
momentum = 0.1        #<--- Állandó lendülettényező
while loss > 0.01:    #<--- Optimalizálási hurok
    w, loss, gradient = get_current_parameters()
    velocity = past_velocity * momentum - learning_rate * gradient
    w = w + momentum * velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)

2.4.4 Deriváltak láncolása: A Backpropagation algoritmus

Az előző algoritmusban véletlenül azt feltételeztük, hogy mivel egy függvény differenciálható, könnyen ki tudjuk számítani a gradiensét. De igaz ez? Hogyan számíthatjuk ki a gyakorlatban az összetett kifejezések gradiensét? A kétrétegű modellben azzal kezdtük a fejezetet, hogy hogyan kaphatjuk meg a veszteség gradiensét a súlyok tekintetében. Itt jön be a Backpropagation algoritmus.

A LÁNCSZABÁLY

A (hiba)visszaterjesztés egy módja annak, hogy egyszerű műveletek deriváltjait (például összeadás, relu vagy tenzorszorzat) használjuk ezen atomi műveletek tetszőlegesen összetett kombinációinak gradiensének egyszerű kiszámításához. Lényeges, hogy egy neurális hálózat sok, egymáshoz láncolt tenzorműveletből áll, amelyek mindegyikének van egy egyszerű, ismert származéka. Például a 2.2-es listában definiált modell kifejezhető a W1, b1, W2 és b2 változókkal paraméterezett függvényként (amelyek az első és a második Dense réteghez tartoznak), és amely magában foglalja a dot, relu, softmax és + atomi műveleteket, valamint a loss veszteségfüggvényünket, amelyek mindegyike könnyen differenciálható:

loss_value = loss(y_true, softmax(dot(relu(dot(inputs, W1) + b1), W2) + b2))

A calculus azt mondja, hogy egy ilyen függvénylánc származtatható a következő azonosság, az úgynevezett láncszabály segítségével. Tekintsünk két f és g függvényt, valamint az összeállított fg függvényt úgy, hogy fg(x) == f(g(x)):

def fg(x):
    x1 = g(x)
    y = f(x1)
    return y

Ekkor a láncszabály kimondja, hogy grad(y, x) == grad(y, x1) * grad(x1, x). Ez lehetővé teszi az fg deriváltjának kiszámítását mindaddig, amíg ismeri f és g deriváltjait. A láncszabály elnevezése azért van így, mert ha további köztes függvényeket ad hozzá, láncnak kezd kinézni:

def fghj(x):
    x1 = j(x)
    x2 = h(x1)
    x3 = g(x2)
    y = f(x3)
    return y

grad(y, x) == (grad(y, x3) * grad(x3, x2) *
               grad(x2, x1) * grad(x1, x))

A láncszabály alkalmazása a neurális hálózat gradiensértékeinek kiszámítására egy visszaterjesztésnek nevezett algoritmust eredményez. Lássuk, hogyan működik ez konkrétan.

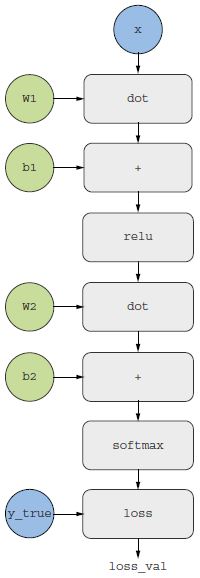
2.21. ábra: A kétrétegű modellünk számítási gráfja

AUTOMATIKUS DIFFERENCIÁLÁS SZÁMÍTÁSI GRÁFOKKAL

A visszaterjesztés hasznos módja a számítási gráfok használata. A számítási gráf a TensorFlow és általában a mélytanulási forradalom középpontjában álló adatstruktúra. Ez a műveletek irányított aciklikus gráfja – esetünkben tenzorműveletek. Például a 2.21. ábra az első modellünk gráfos ábrázolását mutatja.

A számítási gráfok rendkívül sikeres absztrakciót jelentenek a számítástechnikában, mert lehetővé teszik számunkra, hogy a számítást adatként kezeljük: egy kiszámítható kifejezést géppel olvasható adatstruktúraként kódolnak, amely egy másik program bemeneteként vagy kimeneteként használható. Például elképzelhetünk egy programot, amely számítási gráfot kap, és egy új számítási gráfot ad vissza, amely ugyanazon számítás nagy léptékű elosztott változatát valósítja meg – ez azt jelentené, hogy bármilyen számítást eloszthat anélkül, hogy magának kellene megírnia az elosztási logikát. Vagy képzeljünk el egy programot, amely egy számítási gráfot kap, és automatikusan generálja az általa reprezentált kifejezés deriváltját. Sokkal egyszerűbb ezeket a dolgokat megtenni, ha a számításokat explicit gráf adatstruktúraként fejezik ki, nem pedig mondjuk ASCII-karakterek soraiban egy .py fájlban.

A visszaterjesztés egyértelmű magyarázata érdekében nézzünk meg egy igazán alapvető példát egy számítási gráfra (lásd a 2.22. ábrát). A 2.21. ábra egyszerűsített változatát tekintjük, ahol csak egy lineáris rétegünk van, és ahol minden változó skaláris. Vegyünk két w és b skalárváltozót, egy x skaláris bemenetet, és alkalmazunk rájuk néhány műveletet, hogy y kimenetté egyesítsük őket. Végül egy abszolút érték-hibaveszteség függvényt alkalmazunk: loss_val = abs(y_true - y). Mivel a w-t és a b-t úgy szeretnénk frissíteni, hogy az minimalizálja a loss_val értékét, a grad(loss_val, b) és a grad(loss_val, w) kiszámítása érdekel.

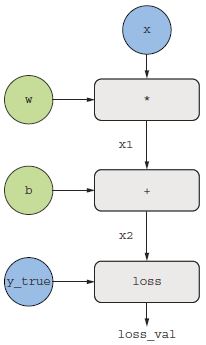
2.22. ábra: A számítási gráf alapvető példája

Adjunk meg konkrét értékeket a gráf „bemeneti csomópontjaihoz”, azaz az x bemenethez, a cél y_true, w és b pontokhoz. Ezeket az értékeket a gráf összes csomópontjára továbbítjuk, felülről lefelé, amíg el nem érjük a loss_val pontot. Ez az előre passz (lásd a 2.23. ábrát).

Most „fordítsuk meg” a gráfot: a gráf minden éléhez, amely A-ból B-be megy, létrehozunk egy ellentétes élt B-től A-ig, és megkérdezzük, mennyiben változik B, amikor A változik? Vagyis mi az a grad(B, A)? Ezzel az értékkel minden fordított élt megjelölünk. Ez a visszafelé gráf ábrázolja a vissza passz (lásd a 2.24. ábrát). ​

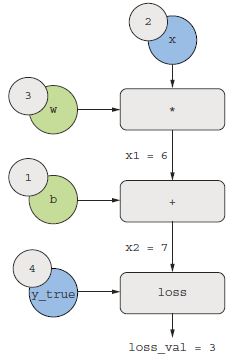
2.23. ábra: Az előrepassz futása

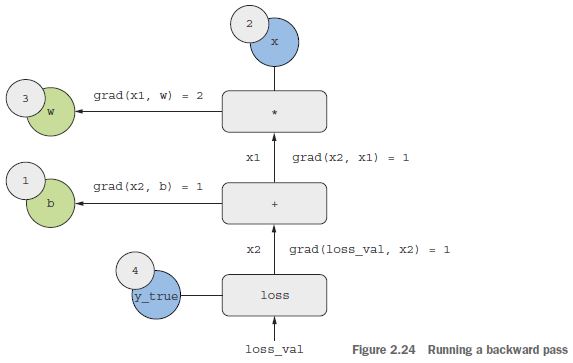
2.24. ábra: A hátrapassz futása

A következőket kaptuk:

A láncszabály azt mondja erről a visszafelé mutató gráfról, hogy úgy tudjuk megkapni egy csomópont deriváltját egy másik csomóponthoz képest, ha megszorozzuk a deriváltakat a két csomópontot összekötő útvonal minden élére. Például grad(loss_val, w) = grad(loss_val, x2) * grad(x2, x1) * grad(x1, w) (lásd a 2.25. ábrát).

2.25. ábra: Útvonal a loss_val és w között a visszafelé mutató gráfon

A láncszabályt a gráfunkra alkalmazva megkapjuk, amit kerestünk:

 grad(loss_val, w) = 1 * 1 * 2 = 2
 grad(loss_val, b) = 1 * 1 = 1

MEGJEGYZÉS

Ha több útvonal köti össze a két érdekes csomópontot, a-t és b-t, a visszafelé mutató gráfban, akkor a grad(b, a) értéket az összes útvonal hozzájárulásának összegzésével kapjuk meg.

És ezzel éppen a visszaterjesztést láttad működés közben! A visszaterjesztés egyszerűen a láncszabály alkalmazása egy számítási gráfra. Nincs benne több. A visszaterjesztés a végső veszteségértékkel kezdődik, és visszafelé halad a felső rétegektől az alsó rétegekig, kiszámítva az egyes paraméterek hozzájárulását a veszteségértékhez. Innen származik a „backpropagation” elnevezés: „visszaterjesztjük” a különböző csomópontok veszteség-hozzájárulását egy számítási gráfban.

Manapság az emberek a neurális hálózatokat olyan modern keretrendszerekben valósítják meg, amelyek képesek az automatikus differenciálásra, mint például a TensorFlow. Az automatikus differenciálás az imént látott számítási gráffal valósul meg. Az automatikus differenciálás lehetővé teszi a differenciálható tenzorműveletek tetszőleges kompozícióinak gradienseinek lekérését anélkül, hogy az előrelépés lejegyzésén túl további munkát végeznénk. Amikor a 2000-es években megírtam az első neurális hálózataimat C nyelven, kézzel kellett megírnom a gradienseimet. Most, a modern automatikus differenciáló eszközöknek köszönhetően soha nem kell saját magadnak megírnod a visszaterjesztést. Tekintsd magad szerencsésnek!

A GRADIENS SZALAG TENSORFLOW-BAN

Az API, amelyen keresztül ki tudjuk használni a TensorFlow erőteljes automatikus differenciálási képességeit, a GradientTape. Ez egy Python hatókör, amely „rögzíti” a benne futó tenzorműveleteket számítási gráf formájában (ezt néha „szalagnak” is nevezik). Ez a gráf ezután felhasználható bármely kimenet gradiensének lekérésére bármely változóhoz vagy változóhalmazhoz (a tf.Variable osztály példányaihoz). A tf.Variable egy speciális tenzorfajta, amely változtatható állapot tárolására szolgál – például egy neurális hálózat súlyai mindig tf.Variable példányok.

import tensorflow as tf
x = tf.Variable(0.)               #<--- Példányosítunk egy skalárváltozót, amelynek kezdeti értéke 0.
with tf.GradientTape() as tape:   #<--- Megnyitunk egy GradientTape hatókört.
    y = 2 * x + 3                 #<--- A hatókörön belül alkalmazunk néhány tenzorműveletet a változónkra.
grad_of_y_wrt_x = tape.gradient(y, x)   #<--- A szalagot használjuk az y kimenet
                                        #     gradiensének lekéréséhez az x változó függvényében.

A GradientTape működik tenzorműveletekkel:

x = tf.Variable(tf.random.uniform((2, 2)))  #<--- Példányosít egy olyan változót, amelynek alakja (2, 2) és kezdőértéke csupa nulla.
with tf.GradientTape() as tape:
    y = 2 * x + 3
grad_of_y_wrt_x = tape.gradient(y, x)   #<--- A grad_of_y_wrt_x egy (2, 2) alakú tenzor (mint az x),
                                        #     amely leírja az y = 2 * a + 3 görbületét x = [[0, 0], [0, 0]] körül.

Változólistákkal is működik:

W = tf.Variable(tf.random.uniform((2, 2)))
b = tf.Variable(tf.zeros((2,)))
x = tf.random.uniform((2, 2))
with tf.GradientTape() as tape:
    y = tf.matmul(x, W) + b                       #<--- matmul az, ahogyan a „dot product”-ot mondjuk TensorFlow-ban.
grad_of_y_wrt_W_and_b = tape.gradient(y, [W, b])  #<--- A grad_of_y_wrt_W_and_b két olyan tenzor listája,
                                                  #     amelyek ugyanolyan alakúak, mint W és b, rendre.

A következő fejezetben fogjuk megtanulni a gradiens szalagot. {61.o:}

2.5 Visszatekintés az első példánkra

Ennek a fejezetnek a végéhez közeledünk, és most már általánosan meg kellett értenie, mi történik a neurális hálózat színfalai mögött. Ami a fejezet elején egy varázslatos fekete doboz volt, az tisztább kép lett, amint azt a 2.26. ábra szemlélteti: a modell, amely egymáshoz láncolt rétegekből áll, a bemeneti adatokat előrejelzésekre képezi le. A veszteségfüggvény ezután összehasonlítja ezeket az előrejelzéseket a célokkal, és veszteségi értéket állít elő: azt méri, hogy a modell előrejelzései mennyire egyeznek a várttal. Az optimalizáló ezt a veszteségi értéket használja fel a modell súlyainak frissítéséhez.

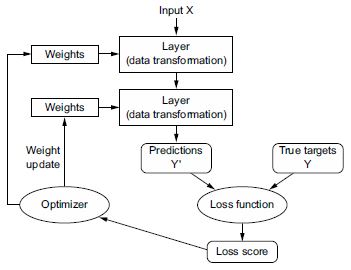
2.26. ábra: A hálózat, a rétegek, a veszteségfüggvény és az optimalizáló közötti kapcsolat

Térjünk vissza a fejezet első példájához, és tekintsük át annak minden egyes részét az azóta tanultak fényében.

Ez volt a bemeneti adat:

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255

Most már megérti, hogy a bemeneti képek NumPy tenzorokban vannak tárolva, amelyek itt float32 tenzorok, melyek alakja (60000, 784) (a képzési adatok) és (10000, 784) (a tesztadatok).

Ez volt a mi modellünk:

model = keras.Sequential([
    layers.Dense(512, activation="relu"),
    layers.Dense(10, activation="softmax")
])

Most már megérti, hogy ez a modell két Dense rétegből álló láncból áll, hogy mindegyik réteg néhány egyszerű tenzorműveletet alkalmaz a bemeneti adatokra, és ezek a műveletek súlytenzorokat tartalmaznak. Súlytenzorok, amelyek a rétegek attribútumai, ott vannak, ahol a modell ismerete megmarad.

Ez volt a modell-összeállítás lépése:

model.compile(optimizer="rmsprop",
              loss="sparse_categorical_crossentropy",
              metrics=["accuracy"])

Most már megértette, hogy a sparse_categorical_crossentropy az a veszteségfüggvény, amelyet visszacsatolási jelként használnak a súlytenzorok megtanulásához, és amelyet a képzési szakasz megpróbál minimalizálni. Azt is tudja, hogy ez a veszteségcsökkentés mini-batch sztochasztikus gradiens ereszkedés révén történik. A gradiens ereszkedés konkrét használatát szabályozó pontos szabályokat az első argumentumként átadott rmsprop optimalizáló határozza meg.

Végül ez volt a képzési ciklus:

model.fit(train_images, train_labels, epochs=5, batch_size=128)

Most már érti, mi történik, ha meghívjuk a fit-et: a modell 128 mintából álló mini kötegekben kezdi el iterálni a betanítási adatokat, ötször (az összes betanítási adat minden egyes iterációját epoch-nak/betanítási szakasznak nevezzük). A modell minden kötegnél kiszámítja a veszteség gradiensét a súlyok figyelembevételével (a Backpropagation algoritmus használatával, amely a számítási láncszabályból származik), és a súlyokat abba az irányba mozgatja, amely csökkenti a veszteség értékét erre a kötegre.

Ezen 5 szakasz után a modell 2345 gradiens-frissítést hajtott végre (szakaszonként 469-et), és a modell vesztesége kellően kicsi lett ahhoz, hogy a modell képes legyen nagy pontossággal osztályozni a kézzel írt számjegyeket.

Ezen a ponton már tudjuk a legtöbbet, amit a neurális hálózatokról tudni lehet. Bizonyítsuk be ezt az első példa egyszerűsített változatának újbóli, lépésről lépésre „a semmiből” való megvalósításával a TensorFlow-ban. {63.o:}

2.5.1 Az első példánk újbóli megvalósítása a semmiből TensorFlow-ban

Mi bizonyítja jobban a teljes, egyértelmű megértést, mint mindent a semmiből valósítani meg? Természetesen az, hogy itt mit jelent a „semmiből/nulláról”, relatív: nem fogjuk újra megvalósítani az alapvető tenzorműveleteket, és nem implementáljuk a visszaterjesztést. De olyan alacsony szintre fogunk menni, hogy szinte egyáltalán nem fogjuk használni a Keras függvényeit.

Ne aggódjon, ha még nem érti ennek a példának minden apró részletét. A következő fejezet részletesebben foglalkozik a TensorFlow API-val. Egyelőre csak próbálja meg követni a folyamat lényegét – ennek a példának az a célja, hogy segítsen kikristályosítani a mélytanulás matematikájának megértését egy konkrét megvalósítás segítségével. Gyerünk!

EGY EGYSZERŰ Dense OSZTÁLY

Korábban már megtanulta, hogy a Dense réteg az alábbi bemeneti transzformációt valósítja meg, ahol W és b modellparaméterek, az activation pedig elemenkénti függvény (általában relu, de ez a softmax lenne az utolsó réteghez):

output = activation(dot(W, input) + b)

Valósítsunk meg egy egyszerű Python osztályt, a NaiveDense-t, amely két TensorFlow változót, W-t és b-t hoz létre, és nyújt egy __call__() metódust, amely alkalmazza az előző transzformációt.

import tensorflow as tf

class NaiveDense:
    def __init__(self, input_size, output_size, activation):
        self.activation = activation

        w_shape = (input_size, output_size)     #<--- Létrehozunk egy W mátrixot (input_size, output_size)
                                                #     méretben, véletlenszerű értékekkel inicializálva.
        w_initial_value = tf.random.uniform(w_shape, minval=0, maxval=1e-1)
        self.W = tf.Variable(w_initial_value)

        b_shape = (output_size,                 #<--- Létrehozunk egy b vektort (output_size,) méretben,
                                                #     nullákkal inicializálva.
        b_initial_value = tf.zeros(b_shape)
        self.b = tf.Variable(b_initial_value)

    def __call__(self, inputs)::                #<--- Alkalmazza az előre passzt.
        return self.activation(tf.matmul(inputs, self.W) + self.b)

    @property
    def weights(self):            #<--- Kényelmes módszer a réteg súlyainak lekéréséhez​
        return [self.W, self.b]

EGY EGYSZERŰ Sequential OSZTÁLY

Most hozzunk létre egy NaiveSequential osztályt ezeknek a rétegeknek a láncolásához. Becsomagolja a fóliák listáját, és megjelenít egy __call__() metódust, amely egyszerűen meghívja az alatta lévő rétegeket a bemeneteken, sorrendben. Ezenkívül tartalmaz egy weights tulajdonságot is, hogy könnyen nyomon követhessük a rétegek paramétereit. {64.o:}

class NaiveSequential:
    def __init__(self, layers):
        self.layers = layers

    def __call__(self, inputs):
        x = inputs
        for layer in self.layers:
            x = layer(x)
        return x

    @property
    def weights(self):
        weights = []
        for layer in self.layers:
            weights += layer.weights
        return weights

Ennek a NaiveDense osztálynak és a NaiveSequential osztálynak a használatával létre tudunk hozni egy ál Keras modellt:

model = NaiveSequential([
    NaiveDense(input_size=28 * 28, output_size=512, activation=tf.nn.relu),
    NaiveDense(input_size=512, output_size=10, activation=tf.nn.softmax)
])
assert len(model.weights) == 4

KÖTEG GENERÁTOR

Ezután szükségünk van egy módszerre az MNIST adatok mini kötegekben történő iterálására. Ez könnyű:

import math

class BatchGenerator:
    def __init__(self, images, labels, batch_size=128):
        assert len(images) == len(labels)
        self.index = 0
        self.images = images
        self.labels = labels
        self.batch_size = batch_size
        self.num_batches = math.ceil(len(images) / batch_size)

    def next(self):
        images = self.images[self.index : self.index + self.batch_size]
        labels = self.labels[self.index : self.index + self.batch_size]
        self.index += self.batch_size
        return images, labels

2.5.2 Egy tréning lépés lefutása

A folyamat legnehezebb része a „képzési lépés”: a modell súlyozásának frissítése egy adatkötegen való futtatás után. Ehhez muszáj

  1. kiszámítani a modell előrejelzéseit a kötegben lévő képekhez;
  2. kiszámítani ezeknek az előrejelzéseknek a veszteségértékét a tényleges címkék alapján;
  3. kiszámítani a veszteség gradiensét a modell súlyai alapján;
  4. mozgatni a súlyokat egy kis mértékben a gradienssel ellentétes irányba.

A gradiens kiszámításához a TensorFlow GradientTape objektumot használjuk, amelyet a 2.4.4 szakaszban mutattunk be:

def one_training_step(model, images_batch, labels_batch):
    #--- Futtassa az „előrelépést” (számítsa ki a modell előrejelzéseit a GradientTape hatókörben):
    with tf.GradientTape() as tape:
        predictions = model(images_batch)
        per_sample_losses = tf.keras.losses.sparse_categorical_crossentropy(
            labels_batch, predictions)
        average_loss = tf.reduce_mean(per_sample_losses)
    gradients = tape.gradient(average_loss, model.weights)    #<--- Számítsuk ki a veszteség gradiensét
                                                              #     a súlyok figyelembevételével!
                                                              #     A kimeneti gradients egy lista, ahol minden bejegyzés
                                                              #     egy súlynak felel meg a model.weights listából.
    update_weights(gradients, model.weights)    #<--- Frissítsük a súlyokat a gradients segítségével
                                                #     (ezt a függvényt hamarosan meghatározzuk).
    return average_loss

Mint már tudja, a „súlyfrissítés” lépés célja (amelyet az előző update_weights függvény képvisel) az, hogy a súlyokat „egy kicsit” olyan irányba mozgassa, amely csökkenti a veszteséget ebben a kötegben. A mozgás nagyságát a „tanulási ráta” határozza meg, ami jellemzően kis érték. Az update_weights függvény megvalósításának legegyszerűbb módja, ha mindegyik súlyozásból kivonjuk a gradient * learning_rate értéket:

learning_rate = 1e-3

def update_weights(gradients, weights):
    for g, w in zip(gradients, weights):
        w.assign_sub(g * learning_rate)   #<--- Az assign_sub a TensorFlow változók esetén a -= megfelelője.

A gyakorlatban szinte soha nem hajtanánk végre egy ilyen súlyfrissítési lépést kézzel. Ehelyett egy Keras Optimizer példányt használnánk, például:

from tensorflow.keras import optimizers

optimizer = optimizers.SGD(learning_rate=1e-3)

def update_weights(gradients, weights):
    optimizer.apply_gradients(zip(gradients, weights))

Most, hogy a kötegenkénti képzési lépésünk kész, továbbléphetünk a képzés teljes korszakának megvalósítására.

2.5.3 A teljes képzési ciklus

A képzés egy korszaka egyszerűen abból áll, hogy megismételjük a betanítási lépést a betanítási adatok mindegyik kötegére, és a teljes képzési ciklus egyszerűen egy korszak ismétlése:

def fit(model, images, labels, epochs, batch_size=128):
    for epoch_counter in range(epochs):
        print(f"Epoch {epoch_counter}")
        batch_generator = BatchGenerator(images, labels)
        for batch_counter in range(batch_generator.num_batches):
            images_batch, labels_batch = batch_generator.next()
            loss = one_training_step(model, images_batch, labels_batch)
            if batch_counter % 100 == 0:
                print(f"loss at batch {batch_counter}: {loss:.2f}")

Teszteljük:

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255

fit(model, train_images, train_labels, epochs=10, batch_size=128)

2.5.4 A modell kiértékelése

A modellt úgy tudjuk értékelni, hogy a tesztképekre átvesszük az előrejelzéseinek argmax-át, és összehasonlítjuk a várt címkékkel:

predictions = model(test_images)
predictions = predictions.numpy()     #<--- A .numpy() meghívása egy TensorFlow tenzorra
                                      #     átalakítja azt NumPy tenzorrá.
predicted_labels = np.argmax(predictions, axis=1)
matches = predicted_labels == test_labels
print(f"accuracy: {matches.mean():.2f}")

Minden kész! Amint látjuk, elég sok munka “kézzel” elvégezni, amit néhány sor Keras kóddal meg tudunk tenni. De mivel ezeken a lépéseken keresztül ment, most kristálytisztán meg kell értenie, mi történik a neurális hálózaton belül, amikor a fit()-et hívja. Ha rendelkezik ezzel az alacsony szintű mentális modellel arról, amit a kód a színfalak mögött csinál, akkor jobban ki tudja majd használni a Keras API magas szintű szolgáltatásait.

Összegzés

This site is open source. Improve this page.